Доступ: Анонимный

ТЕРЕНИН Алексей Алексеевич, кандидат технических наук

Криптографические алгоритмы, применяемые для обеспечения информационной безопасности при взаимодействии в ИНТЕРНЕТ

Представлены краткий обзор самых распространенных алгоритмов шифрования на сегодняшний день, их описание, а также возникающие проблемы при их реализации и значимые аспекты при практическом использовании.

Защита информации методами криптографического преобразования заключается в изменении ее составных частей (слов, букв, слогов, цифр) с помощью специальных алгоритмов либо аппаратных решений и кодов ключей, то есть в приведении ее к неявному виду. Для ознакомления с шифрованной информацией применяется обратный процесс: декодирование (дешифрование). Использование криптографии является одним из распространенных методов, значительно повышающих безопасность передачи данных в сетях ЭВМ, данных, хранящихся в удаленных устройствах памяти, а также при обмене информацией между удаленными объектами.

Для преобразования (шифрования) обычно используются некоторый алгоритм или устройство, реализующее заданный алгоритм, который может быть известен широкому кругу лиц. Управление процессом шифрования осуществляется с помощью периодически меняющегося кода ключа, обеспечивающего каждый раз оригинальное представление информации при использовании одного и того же алгоритма или устройства. Знание ключа позволяет просто и надежно расшифровать текст. Однако без знания ключа эта процедура может быть практически невыполнима даже при известном алгоритме шифрования.

Даже простое преобразование информации является весьма эффективным средством, дающим возможность скрыть ее смысл от большинства неквалифицированных нарушителей.

Краткий исторический обзор развития шифрования

Появление криптографии восходит к египетским иероглифам. Еще с древнейших времен, когда процветали Египет и Персия, для важнейших государственных и военных поручений использовались посыльные, которые несли текст послания либо на пергаменте, либо у себя в голове, чтобы передать его на словах, последний способ был более предпочтителен. Уже тогда появлялись более или менее успешные способы защиты передаваемой информации от посягательств перехватчиков. Приведем известную легенду из Древнего мира. Некий царь, попав в плен, сделал татуировку на голове раба – сообщение союзникам. Когда отросли волосы, раб перебрался к адресатам сообщения и царь был освобожден. Прообраз нынешней стеганографии.

Древние греки применяли круглые палочки одинакового диаметра, на которые наматывались полоски пергамента. Надпись производилась продольно по длине палочки. Сложить текст в читаемый можно было, только обладая палочкой такого же диаметра.

В Древнем Риме уже начинает явно формироваться наука криптография, переводимая с латыни, как тайнопись. Появляется шифр Цезаря, когда каждая буква заменяется на букву, отстоящую на три по алфавиту.

В средневековой интриганской Европе и Средней Азии, происходит бурное развитие криптографии, и криптоанализа – методов вскрытия шифрованных текстов. Первой систематической работой по криптографии считают книгу архитектора Леона Баттисти Альберти (1404 - 1472). Одним из первых криптоаналитиков был Франсуа Виет (1540 - 1603), при дворе короля Франции Генриха IV. В то же время при дворе папы римского служили советники из семейства Аддженти, которых также можно назвать криптоаналитиками. Весь период до середины XVII в. насыщен работами по криптографии и криптоанализу.

В XIX и в первой половине XX в. для тайной дипломатической переписки многими странами, в том числе и Россией, применяются методы шифрования, ключи для которых составлялись из отрывков определенных текстов обычных книг (шифровальные книги).

С начала ХХ в. - с Первой мировой войны - начинают применяться специальные шифровальные машины.

Широко известна немецкая машина Enigma, код которой был раскрыт англичанами. Чтобы не выдавать факта раскрытия немецкого шифра, английское правительство пошло на большие жертвы среди мирного населения, не предупредив жителей двух крупных городов о готовящихся бомбардировках. Но это помогло затем получить существенный перевес в северных морских сражениях с Германией, когда уничтожались непобедимые немецкие подводные лодки и крейсеры.

После Второй мировой войны криптографией занялись вычислительные машины. Долгое время это был удел мощнейших для своего времени суперкомпьютеров.

Публикации по этой теме были строго засекреченными и использование научных исследований в данной области являлись внутригосударственной прерогативой. Общедоступной была только хрестоматийная работа Фон-Неймана 40-х гг., описывающая, кроме принципов построения вычислительных систем, еще некоторые возможные злоумышленные методы воздействия для нарушения “легального” вычислительного процесса, а также классическая работа Шеннона, заложившая основы компьютерной криптографии.

С 70-х гг. появляются открытые публикации: Хэффи-Дилман в 1976 г. В 1970 г. существовало засекреченное изобретение Джеймса Эллиса (Великобритания) в области криптографии. Наиболее известный алгоритм асимметричной криптографии – RSA, разработанный Рональдом Ривестом, Эдди Шамиром и Леном Эдлеманом в 1977 г. Алгоритм RSA имеет большое значение, т.к. может использоваться как для шифрования с открытым ключом, так и для создания электронной цифровой подписи.

Это был революционный период в развитии криптографической науки. Появились новейшие методы секретного распространения ключевой информации в открытых вычислительных системах, а также родилась несимметричная криптография.

Но и после этого долгое время прерогатива использования криптографии в защите данных была у государственных служб и крупных корпораций. Вычислительная техника того времени, обладающая мощностью, необходимой для криптографических преобразований была очень дорогостоящей.

В то время появляются основные государственные стандарты криптографических алгоритмов (США и некоторые европейские страны), использование которых предписывалось при работе с информацией, отнесенной к государственной тайне.

Завеса секретности вокруг этих технологий привела даже к тому, что в США криптографические алгоритмы были приравнены к вооружению, был введен запрет на вывоз шифровальных аппаратных и программных средств. Затем были введены экспортные ограничения на длину используемого ключа в алгоритмах шифрования за пределами США, что позволяло американским спецслужбам производить дешифрацию сообщений на имеющихся вычислительных мощностях без знания укороченного ключа. С 1 марта 2001 г. экспортные ограничения были сняты. Из-за событий, произошедших 11 сентября того же года, наблюдается ужесточение государственного контроля. Правительство США рассматривает варианты обратного введения экспортного контроля над средствами шифрования.

Вернемся в 70-е гг. С того времени ни научные изыскания, ни развитие вычислительных средств не останавливались. Вычислительные мощности суперкомпьютеров возрастают в несколько раз каждые несколько лет. Появляется персональный компьютер. Мощность персонального компьютера приблизительно равна мощности суперкомпьютера десятилетней давности. Сейчас персональные компьютеры стали еще мощнее.

С 80-х гг. у простых пользователей появляется возможность использовать криптографические средства на своих компьютерах, чему яростно препятствуют государственные органы, становится сложнее осуществлять наблюдение за деятельностью граждан страны, в том числе и за преступными элементами.

Выход в свет программы PGP (Pretty Good Privacy) Фила Циммерманна (версия 1.0 вышла в 1991 г.) и предоставление ее в открытое и бесплатное использование дали большие возможности рядовым компьютерным пользователям. Фила Циммерманна даже объявили врагом государства, он был приговорен к лишению свободы.

Постоянно возрастающие вычислительные мощности заставляли использовать все более сложные алгоритмы криптопреобразования или увеличивать длину ключей, используемых при шифровании.

Стандарты на криптографические алгоритмы устаревали, становились ненадежными. Информация, закрытая на некотором ключе, уже не могла храниться конфиденциально достаточно долго - столько, сколько полагалось по государственным нормам. Например, хранение информации в полном секрете в зашифрованном виде в течение 5 лет означало, что противник, обладая самыми мощными вычислительными средствами, постоянно перебирая возможные ключи, за этот срок с достаточно большой вероятностью не подобрал бы нужный ключ для расшифрования хранимой информации.

Стали проводиться конкурсы на вскрытие некоторой информации, зашифрованной по алгоритму одного из стандартов. Победителю назначался солидный денежный приз, а также всемирная слава в информационном сообществе. Объединяя обыкновенные компьютеры в вычислительной сети для параллельной работы над решением данной задачи, пользователи собирались в группы и подбирали ключ сообща.

Длина ключа 48 бит означает, что необходимо сделать 2⁴⁸ переборов. Увеличение длины ключа, например, всего на 16 бит, означает, что перебрать необходимо в 2¹⁶ раз больше.

Но даже такой размер ключа позволял решить проблему вскрытия шифра объединенным группам за дни и даже за часы параллельной работы. В дальнейшем потребовался переход на ключи, которые в несколько раз длиннее упомянутых. Но и это была только временная мера, и недавно были приняты новые стандарты на алгоритмы криптопреобразований (AES в США).

В настоящее время в прессе появилось множество публикаций, посвященных этой проблеме. Издаются многочисленные книги, как переводные, так и российских авторов. Задачу защиты информации от раскрытия и модификации позволяет решать криптография. Математический аппарат современной криптографии по сложности превосходит тот, который используется для разработки ядерного оружия и космических систем.

Современная криптография делится на симметричную и асимметричную. Симметричная – на потоковый шифр, блочный и составной. Асимметричная криптография более ресурсоемкая, а в симметричной существует проблема эффективного распределения ключей. Современные системы безопасного обмена основаны на применении смешанной криптографии. В начале сеанса обмена стороны пересылают друг другу посредством асимметричной криптографии секретные сеансовые ключи, которые используются далее для симметричного шифрования пересылаемых данных. Система асимметричной криптографии позволяет распределять ключи в симметричных системах шифрования.

В правительственных и военных телекоммуникационных системах используется исключительно симметричное шифрование (чаще всего с использованием одноразовых ключей). Это обусловлено тем, что строго математически не доказана стойкость систем с открытыми ключами, но не доказано и обратное.

Шифрование информации не следует принимать как панацею от всех информационных угроз. Его следует воспринимать как одну из обязательных мер защиты информации в составе комплексной системы обеспечения информационной безопасности. Применение шифрования следует сочетать с законодательными, организационными и другими мерами защиты.

Симметричные алгоритмы шифрования

Алгоритмы шифрования предназначены для решения задачи обеспечения конфиденциальности информации. В настоящее время для закрытия информации интенсивно используются криптографические методы. С древнейших времен наиболее эффективной формой защиты было и остается шифрование.

Шифрование определяется как взаимообратное преобразование незащищенной (открытой) информации в зашифрованную (закрытую) форму – шифртекст [1], в которой она не представлена полностью доступной для злоумышленника. При шифровании используются ключи, наличие которых означает возможность зашифрования и/или расшифрования информации. Важно отметить, что сам метод шифрования не требуется держать в секрете, т. к. знание только его не позволит расшифровать шифртекст.

Современные криптосистемы можно однозначно разделить по способу использования ключей на криптосистемы с секретным ключом (симметричные) и с открытым ключом (асимметричные). Если для зашифрования и расшифрования используется один и тот же ключ, такая криптосистема называется симметричной.

К симметричным криптосистемам относятся DES [2], AES, ГОСТ 28147-89 [3] и т.д. Новым направлением в криптографии стало изобретение асимметричных криптосистем с открытым ключом, таких, как RSA, DSA или Эль-Гамаль [4, 5].

В асимметричных криптосистемах для зашифрования и расшифрования применяют различные, практически не выводимые друг из друга ключи, один из которых (ключ расшифрования) делается секретным, а другой (ключ зашифрования) - открытым. Этим достигается возможность передавать секретные сообщения по незащищенному каналу без предварительной передачи секретного ключа. Именно криптография с открытым ключом разорвала порочный круг симметричных шифров, когда для организации обмена секретной информацией надо было сначала произвести распределение секретных ключей.

Детально криптосистемы с открытым ключом будут рассмотрены далее, а сейчас вернемся к симметричным криптосистемам (КС).

Важнейшей составной частью КС являются шифры [1, 4] или процедуры взаимообратного преобразования открытого текста M в шифртекст M':

M’ = E(M),
M = D(M’),

где E - функция зашифрования и D - функция расшифрования.

Общепринятым подходом в криптографии считается такое построение шифра, при котором его секретность определяется только секретностью ключа K_S (правило Керкоффа). Таким образом, шифр должен быть устойчивым к взлому, даже если потенциальному криптоаналитику известен весь алгоритм шифрования, кроме значения используемого ключа, и он располагает полным текстом перехваченной шифрограммы.

Практика показала, что чем больше известен алгоритм, чем больше людей работало с ним, тем более проверенным, а значит, и надежным он становится. Так, публично известные алгоритмы сейчас выдерживают борьбу со временем, а вот засекреченные государственные шифры обнаруживают в себе множество ошибок и недочетов, т. к. всего учесть невозможно.

Общепринятая схема построения симметричных криптосистем представляет собой циклические перестановки и подстановки битов в блоке фиксированной длины, алгоритм которых определяется секретным ключом.

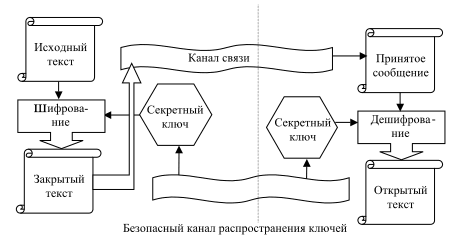
Рис. 1. Схема построения симметричных криптосистем

Алгоритм шифрования считается стойким, если, имея закрытые данные, и зная секретный ключ, невозможно получить информацию об открытых данных. Строго доказана невозможность построения абсолютно стойкого шифра, за исключением случая, когда размер секретного ключа равен (или больше) размеру шифруемых данных [1]. Этот случай трудно реализуем на практике, т.к. реально применяемые и доступные на рынке средства криптографической защиты используют шифры, для которых задача восстановления открытого текста по закрытому является трудно вычислимой, то есть требует настолько больших ресурсов, что атака становится экономически нецелесообразной.

Среди симметричных шифров наиболее известны и часто используемы следующие (размер блока в битах обозначен как b, число циклов- r, а длина ключа - l):

DES - государственный стандарт США [2] (b = 64, r = 16, l = 56). В настоящее время доказана недостаточная стойкость DES против атаки методом простого перебора [6, 7].
Triple DES и DESX (b = 64, r = 16, l = 168;112) - последовательное применение алгоритма DES с разными ключами, что обеспечивает значительную устойчивость к взлому [4, 8, 9].
IDEA - (b = 64, r = 8, l = 128) [4]. Активные исследования его стойкости выявили в нем ряд слабых ключей, однако вероятность их использования пренебрежимо мала.
RC5 - параметризованный шифр с переменными размером блока (b I [32, 64, 128]), количеством циклов (r Ј 255) и числом битов ключа (l Ј 2040) [10]. Исследования его стойкости [11] показали, что при b = 64 он недоступен для дифференциального криптоанализа при r і 12 и для линейного криптоанализа при r і 7.
ГОСТ 28147-89 - российский стандарт шифрования данных [3] (b = 64, r = 32, l = 256). Для ГОСТа было найдено множество слабых ключей, значительно снижающих его эффективную стойкость в простых режимах шифрования [12, 13]. Оценка криптостойкости ГОСТа затруднена также тем фактом, что важнейшая часть алгоритма - узлы замены или S-боксы в терминологии шифра DES - не описана в стандарте и законы ее генерации остаются неизвестными. В то же время доказано, что высока вероятность получения слабых узлов замены, упрощающих криптоанализ данного шифра.
Blowfish - это 64-битовый блочный шифр, разработанный Шнайером (Schneier) в 1993 г., реализуется посредством перестановок и замен, зависимых от ключа. Все операции основаны на операциях XOR и прибавлениях к 32-битовым словам (XORs and additions on 32-bit words). Ключ имеет переменную длину (максимально 448 бит) и используется для генерации нескольких подключевых массивов (subkey arrays). Шифр был создан специально для 32-битовых машин и существенно быстрее DES [14].

Сейчас в США принят новый стандарт шифрования AES. Был проведен конкурс среди алгоритмов шифрования, в котором победил и лег в основу AES – Rijndael. Rijndael представляет собой итеративный блочный шифр, имеющий переменную длину блоков и различные длины ключей. Более подробное описание этого алгоритма и итогов проведения конкурса дано в [18].

В мире разработано, опубликовано и исследовано достаточно большое число симметричных алгоритмов (табл. 1), из которых лишь DES и его модификация Triple DES были достаточно проверены временем. В таблицу не включены малоизвестные и слабоизученные алгоритмы, такие, как Safer, и т.д.

Таблица 1. Обзор симметричных методов шифрования

Метод	Длина ключа, бит	Размер блока, бит	Затраты на подбор ключа, MIPS x лет	Примечание
DES	56	64	5 102	Разработан в 1977 г. фирмой IBM по заказу правительства США. За 20 лет не найдено способа взломать шифр, кроме полного перебора в среднем 25% всех ключей, но при современных возможностях он позволяет достичь успеха [15]
Triple DES	128 (112)	64	1018	Трехкратное повторение алгоритма DES с разными ключами. Эффективная длина ключа 112 бит.
IDEA	128	64	1021	Разработан в 1992 г. Lai и Massey. Не взломан до настоящего времени
ГОСТ 28147-89	256	64	нет данных	Является Государственным стандартом в России
RC5	40 и выше	32 и выше	103 и выше	40-битовый ключ был взломан перебором в 1997 г. за 3,5 ч, 48-битовый ключ - за 313 ч
Blowfish	до 448	64	нет данных	Разработан Шнайером (Schneier) в 1993 г. Это шифр Файстела (Feistel) был создан специально для 32-битовых машин и существенно быстрее DES
AES (Rijndael)	Длина ключа и длина блока могут быть 128, 192 или 256 бит, независимо друг от друга			Предложен криптоаналитиками Joan Daemen и Vincent Rijmen. Алгоритм не имеет известных слабостей в защите (по данным NIST).

В настоящее время симметричные алгоритмы с длиной ключа более 100 бит (Triple DES и IDEA и т.д.) не являются невскрываемыми. Отечественный алгоритм ГОСТ по сравнению с ними отличается повышенной сложностью как при генерации узлов замены, так и при генерации ключей. Также для алгоритма ГОСТ существует большая вероятность генерации нестойкого ключа, что в некоторых режимах шифрования снижает его эффективную длину ключа с 2²⁵⁶ до 2⁶² [12].

Triple DES является более проверенным, чем IDEA алгоритмом и обеспечивает приемлемую скорость работы. Алгоритм Triple DES представляет собой трехкратное применение алгоритма DES к одним данным, но с разными ключами.

В Россию DES проник и достаточно широко практически используется как неотъемлемая деталь различных программных и аппаратных средств, из которых наиболее широко известны система S.W.I.F.T., секретные модули VISA и EUROPAY, секретные модули банкоматов и торговых терминалов и, наконец, смарт-карты. Особенно напряженные дискуссии вокруг алгоритмов шифрования данных вызваны именно смарт-картами. При этом есть серьезные основания считать, что надежность отечественных криптосистем конверсионного происхождения будет превосходить зарубежные аналоги [16].

Однако российское законодательство, впрочем, как и законодательства многих других стран, разрешает лишь использование национальных стандартов шифрования.

Алгоритм ГОСТ 28147-89 построен по тому же принципу, что и DES, это классический блочный шифр с секретным ключом, однако отличается от DES большей длиной ключа, большим количеством раундов и более простой схемой построения самих раундов. В табл. 2 приведены его основные параметры, для удобства - в сравнении с параметрами DES [17].

Таблица 2. Сравнение параметров шифров DES и ГОСТ

Параметр	ГОСТ	DES
Размер блока шифрования	64 бита	64 бита
Длина ключа	256 бит	56 бит
Число раундов	32	16
Узлы замен (S-блоки)	не фиксированы	фиксированы
Длина ключа для одного раунда	32 бита	48 бит
Схема выработки раундового ключа	простая	сложная
Начальная и конечная перестановки битов	нет	есть

Если секретной информацией требуется обмениваться лицам, доверяющим друг другу, т.е. входящим в одну организацию, можно применять средства симметричной криптографии. Конечно, при этом обе (или более) стороны должны уже обладать ключами шифрования для взаимодействия.

Если кратко описать сценарий обмена информации, то он заключается в следующем:

• создается или используется уже существующий файл, содержащий секретную информацию;
• файл зашифровывается на известном обеим сторонам ключе, определенном алгоритмом шифрования;
• зашифрованный файл передается абоненту, носитель информации не так важен, это могут быть дискета, электронная почта, сообщение в сети или связь по модему, очень удобно, для снижения риска, также хранить все файлы, содержащие секретную информацию в зашифрованном виде. Тогда, если, компьютер, ноутбук командированного сотрудника, или жесткий диск попадет в руки злоумышленника, файлы, закрытые ключом, будут недоступны для прямого прочтения. Сейчас в мире используются системы, которые автоматически шифруют всю информацию, хранящуюся в ноутбуке, в них также предусмотрен режим входа по принуждению, если сотрудника заставляют загрузить ноутбук, то, введя специальный пароль, вместо обычного, можно уничтожить всю информацию, естественно, предусмотрен режим восстановления после данного действия. Жесткий диск можно просто демонтировать из компьютера, его не так сложно вынести из охраняемой территории (по сравнению с целым компьютером);
• на приемной стороне законный получатель, обладая ключом, открывает зашифрованные файлы для дальнейшего использования.

Множество современных методов защитных преобразований можно классифицировать на четыре большие группы: перестановки, замены (подстановки), аддитивные и комбинированные методы. Методы перестановки и подстановки обычно характеризуются короткой длиной ключа, а надежность их защиты определяется сложностью алгоритмов преобразования. Для аддитивных методов характерны простые алгоритмы преобразования, а их криптостойкость основана на увеличении длины ключа.

Вскрытие шифра

Существует способ вскрытия шифра, основанный на переборе всех вариантов ключа. Критерием правильности варианта служит наличие в тексте “вероятного слова”.

Перебирается множество всех возможных ключей, шифрованный текст расшифровывается на каждом ключе. В получившемся “псевдооткрытом” тексте ищется вероятное слово. Если такого слова нет, текущий текст бракуется, осуществляется переход к следующему ключу. Если такое слово найдено, на экран выводится вариант ключа. Затем перебор ключей продолжается до тех пор, пока не исчерпается все множество вариантов. Возможно обнаружение нескольких ключей, при которых в “псевдооткрытых текстах” имеется вероятное слово.

После завершения перебора необходимо расшифровать текст на найденных ключах. “Псевдооткрытый текст” выводится на экран для визуального контроля. Если оператор признает текст открытым, то работа по вскрытию заканчивается. Иначе данный вариант ключа бракуется и осуществляется переход к следующему ключу.

Бороться с методом полного перебора позволяет увеличение длины используемого ключа шифрования. Причем, увеличение его длины всего на 8 бит увеличивает число вариантов перебора в 2⁸ раз, соответственно на 64 бита – в 2⁶⁴ раз.

Среди проблем, присущих использованию криптографических алгоритмов шифрования, необходимо выделить проблему распределения ключей. Перед тем как взаимодействующие стороны смогут посылать друг другу зашифрованные сообщения, они должны обменяться ключами шифрования по некоторому секретному каналу. Кроме этого, в системе информационного обмена необходимо поддерживать в актуальном состоянии огромное количество ключей.

Алгоритмы криптографического шифрования не позволяют установить целостность полученного сообщения (т.е. убедиться в том, что при передаче сообщение не было модифицировано). Авторство может быть подтверждено только обладанием определенного ключа, таким образом, любой, кто станет обладателем чужого ключа, сможет выдавать свои сообщения за сообщения, посланные от другого пользователя.

Проблему распределения секретных ключей по общедоступному каналу связи позволяет разрешить алгоритм Диффи-Хелмана. Но данный алгоритм относится к асимметричным криптографическим алгоритмам. В них используются два ключа: открытый и закрытый.

Бурное развитие асимметричные криптоалгоритмы получили в 70-е гг. прошлого столетия. Подобные алгоритмы способны также решить проблемы подтверждения авторства, подлинности, позволяя организовать обмен шифрованной информацией между сторонами, недоверяющими друг другу. Кроме этого, использование асимметричных алгоритмов снижает на порядок количество ключей, которые должны быть распределены между взаимодействующими сторонами. Системы асимметричного шифрования включают общедоступную базу данных открытых ключей, которые могут распределяться по открытым каналам связи и их раскрытие никоим образом не приведет к компрометации системы, поэтому они и называются открытыми.

Асимметричные алгоритмы шифрования

Криптосистемы с открытым ключом строятся, как правило, на основе сложной математической задачи вычисления функции, обратной заданной. Такие функции называются однонаправленными, т.е. их обращение представляет собой практически неразрешимую задачу. Суть метода шифрования в том, что вычисление функции от зашифрованного сообщения в прямом направлении проходит с использованием открытого ключа принимающего абонента, а при расшифровке (вычислении обратной функции) применяется его секретный ключ. Как и следовало ожидать, математических задач, удовлетворяющих перечисленным требованиям, известно немного, и лишь на некоторых из них были построены используемые на практике шифры. Рассмотрим ряд наиболее известных криптосистем с открытым ключом.

• RSA [1]. Используется задача факторизации (вычисления простых сомножителей) большого целого числа. Построен на основе перемножения двух простых чисел большой разрядности [2]. Широко применяется в криптографических протоколах закрытия информации и аутентификации.
• Эль-Гамаль (El-Gamal) [3, 4]. Основан на задаче дискретного логарифмирования в конечном поле [2]. Используется в стандартах электронной цифровой подписи (ЭЦП) DSS [5], ГОСТ Р34.10-94 [6] и т.д.
• Эллиптические кривые (elliptic curve) [7]. Основан на задаче дискретного логарифмирования на эллиптических кривых в конечном поле.

Обратные задачи разложения на множители и дискретного логарифмирования решаются методами, близкими к полному перебору, и при большой разрядности чисел являются трудновычислимыми.
Криптосистемы с открытым ключом используются в основном в трех направлениях:

• закрытие информации;
• аутентификация с использованием ЭЦП;
• защищенное от перехвата распределение открытых ключей (криптосистема Диффи – Хеллмана (Diffie – Hellman)) [8].

Более подробно преимущества и недостатки асимметричных криптосистем рассмотрены в [5, 6, 9, 16, 22, 30, 31].

Хэш-функции

Протоколы защиты целостности и аутентичности при формировании имитовставок и ЭЦП используют криптографические «сжимающие» хэш-функции, позволяющие получить из блока данных произвольной длины значение с фиксированным количеством бит [10, 11, 12, 13, 14, 15].
В целях уменьшения объема ЭЦП и снижения времени на ее формирование и проверку она применяется к хэш-значениям, которые обычно значительно короче исходных сообщений. К криптографическим хэш-функциям предъявляется ряд требований, направленных на затруднение подделки ЭЦП путем нахождения такой модификации блока данных, при которой значение хэш-функции и, следовательно, ЭЦП остаются неизменными.
Наиболее широкое распространение получили следующие хэш-функции, построенные на системе циклически повторяемых перестановок и подстановок (в скобках указана длина вырабатываемого хэш-значения в битах):

• MD5 [16, 17, 18, 19] (128);
• SHA-1 [20] (160);
• ГОСТ [21] (256).

Таблица 1. Перечень и параметры хэш-функций

Хэш-функция	Длина значения, бит	Размер блока, бит	Производительность, Мб/с	Примечание
MD2	128		нет данных	Разработана Роном Ривестом в 1989 г. Обнаружены коллизии в упрощенной функции компрессии [18]
MD4	128	448	23,9	Разработана Роном Ривестом в 1990 г. Обнаружены коллизии [18]
MD5	128	512	16,7	Разработана Роном Ривестом в 1991 г. Обнаружены коллизии в функции компрессии [18]
RIPEMD-160	160		5,67	Разработана в 1995 г. в Европейском проекте RIPE
SHA-1	160	512	6,88	Разработана в 1995 г. в NIST
ГОСТ			0,9	ГОСТ России

В табл. 1 не приведены редко используемые и экзотические хэш-функции, а также хэш-функции, построенные на симметричных блочных шифрах по схемам Мейера – Матиаса (Meyer – Matyas) и Девиса – Прайса (Davies – Price) [9].
Подробнее упомянутые хэш-функции описаны в [11, 16 – 21].
Хотя средства криптографической защиты с «открытым ключом» или асимметричные криптосистемы особенно широко используются начиная с конца 70-х гг. [22], они обладают очень серьезным недостатком – крайне низким быстродействием. В связи с этим на практике обычно используется комбинированная схема криптографической защиты [23]. При установлении соединения и аутентификации сторон используется криптография с «открытым ключом», затем генерируется сеансовый ключ для симметричного шифрования, на котором закрывается весь трафик между абонентами. Сеансовый ключ также распространяется с использованием открытого ключа.

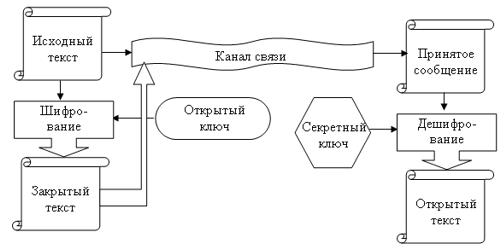
Рис. 2. Схема алгоритма асимметричной криптосистемы

Таблица 2. Асимметричные криптосистемы

Название метода	Метод взлома (мат. проблема)	Криптостойкость, MIPS	Примечание
RSA	факторизация больших простых чисел	2,7•1028 для ключа 1300 бит	Разработан в 1977 г. Роном Ривестом, Ади Шамиром и Леонардом Эйдельманом. Включен во многие стандарты
LUC	факторизация больших простых чисел
El-Gamal (Эль-Гамаль)	нахождение дискретного логарифма в конечном поле	при одинаковой длине ключа криптостойкость равная RSA	Разработан Эль-Гамалем. Используется в алгоритме цифровой подписи DSA-стандарта DSS
Эллиптические уравнения	решение эллиптических уравнений	криптостойкость и скорость работы выше, чем у RSA	Современное направление. Разрабатывается многими ведущими математиками

Метод RSA в настоящее время является стандартом де-факто в системах информационной безопасности и рекомендован CCITT (Consultative Committee in International Telegraphy and Telephony – Международным консультативным комитетом в области телеграфии и телефонии, МККТТ) в стандарте X.509 [24]. RSA используется во многих международных стандартах (S-HTTP, PEM, S-MIME, S/WAN, STT, SSL, PCT, SWIFT, ANSI X.9.31 и т.д.) [24, 25, 26, 27], в системах обслуживания кредитных карточек, в операционных системах для защиты сетевых протоколов.
Для методов RSA и Эль-Гамаля проведено огромное количество научных исследований, изучено большое количество методов их криптоанализа, защиты от атак, детально рассчитана криптостойкость в зависимости от длины ключа и других параметров. Оба метода обладают одинаковой криптостойкостью (при одинаковой длине ключа) и примерно одинаковой скоростью работы. Учитывая, что метод эллиптических уравнений (elliptic curve) проходит стадию апробации и не был подвергнут до настоящего времени такому большому количеству попыток взлома, как методы RSA и Эль-Гамаля, использование в системах шифрования двух последних выглядит предпочтительнее.
Подробное описание данных алгоритмов приведено в [1, 7, 11, 16, 29, 31].

Электронная цифровая подпись

Если информацией обмениваются стороны, не доверяющие друг другу или заинтересованные в проведении действий, направленных друг против друга (банк и клиент, магазин и покупатель), необходимо применять асимметричные методы шифрования, а также метод ЭЦП.
Необходимо обеспечить не только конфиденциальность, но и целостность сообщения (невозможность подменить сообщение или что-то в нем изменить), а также авторство. Кроме этого, необходимо не допустить возможности отказа автора послания от факта отправления подписанного сообщения.
Электронная подпись документа позволяет установить его подлинность. Кроме того, криптографические средства обеспечивают защиту от следующих злоумышленных действий:

• отказ (ренегатство) – абонент А заявляет, что не посылал сообщения Б, хотя на самом деле посылал;
• модификация (переделка) – абонент Б изменяет документ и утверждает, что данный документ (измененный) получил от абонента А;
• подмена – абонент Б формирует документ (новый) и заявляет, что получил его от абонента А;
• активный перехват – нарушитель (подключившийся к сети) перехватывает документы (файлы) и изменяет их;
• «маскарад» – абонент В посылает документ от имени абонента А;
• повтор – абонент В повторяет ранее переданный документ, который абонент А послал абоненту Б.

Все перечисленный виды злоумышленных действий наносят существенный ущерб. Кроме того, возможность злоумышленных действий подрывает доверие к компьютерной технологии [28, 29]. Проблему аутентификации можно решить на основе криптографического подхода, разработав специальные алгоритмы и программы.
При выборе алгоритма и технологии аутентификации необходимо предусмотреть надежную защиту от всех вышеперечисленных видов злоумышленных действий (угроз). Однако в рамках классической (одноключевой) криптографии тяжело защититься от всех приведенных видов угроз, поскольку имеется принципиальная возможность злоумышленных действий одной из сторон, владеющей секретным ключом.
Никто не может помешать абоненту, например, сгенерировать любой документ, зашифровать его на имеющемся ключе, общем для клиента и банка, потом заявить, что он получил этот документ от законного передатчика.
Эффективным является использование схем, основанных на двухключевой криптографии [29]. В этом случае каждый передающий абонент имеет свой секретный ключ подписи, а у всех абонентов есть несекретные открытые ключи передающих абонентов.
Эти открытые ключи можно трактовать как набор проверочных соотношений, позволяющих судить об истинности подписи передающего абонента, но не позволяющих восстановить секретный ключ подписи. Передающий абонент несет единоличную ответственность за свой секретный ключ. Никто, кроме него, не в состоянии сгенерировать корректную подпись. Секретный ключ передающего абонента можно рассматривать как личную печать, и владелец должен всячески ограничивать доступ к нему посторонних лиц. [28].
Для практического воплощения идеи открытого шифрования требовалось найти конкретные и конструктивные ответы на следующие вопросы:

• как «замешивать» индивидуальный ключ пользователя с содержимым документа, чтобы они стали неразделимы?
• как проверить, что содержание подписываемого документа и индивидуальный ключ пользователя подлинны, не зная заранее ни того, ни другого?
• как обеспечить возможность многократного использования автором одного и того же индивидуального ключа для цифровой подписи большого количества электронных документов?
• как гарантировать невозможность восстановления индивидуального ключа пользователя по любому количеству подписанных с его помощью электронных документов?
• как гарантировать подлинность проверки цифровой подписи и содержимого электронного документа?
• как обеспечить юридическую полноправность электронного документа с цифровыми подписями, существующего без бумажного дубликата или другого заменителя?

Для ответа на все эти вопросы потребовалось около 20 лет с того момента, как эта идея была впервые сформулирована в 1976 г. в статье Уитфилда Диффи и Мартина Хеллмана. Сейчас уже можно определенно сказать, что все эти вопросы решены: есть полный арсенал технических средств авторизации электронных документов, называемых цифровой подписью. Современные принципы построения системы цифровой подписи просты и изящны:

• методы вычисления и проверки цифровых подписей всех пользователей системы одинаковы и основываются на широко известных математических задачах;
• методы вычисления ключей проверки цифровых подписей и индивидуальных ключей генерации цифровых подписей также одинаковы для всех и хорошо известны;
• индивидуальные ключи генерации цифровых подписей выбираются самими пользователями по случайному закону из большого множества всех возможных ключей;
• при конкретном алгоритме цифровой подписи его стойкость может быть оценена без привлечения какой-либо «закрытой» информации на основе только известных математических результатов и разумных допущений о вычислительных мощностях потенциального взломщика.

Средства криптографической защиты обеспечивают подлинность и аутентичность информации, кроме решения проблемы сохранения ее конфиденциальности. Данные функции выполняет технология цифровой подписи [6].
Схема работы цифровой подписи изображена на рис. 3.

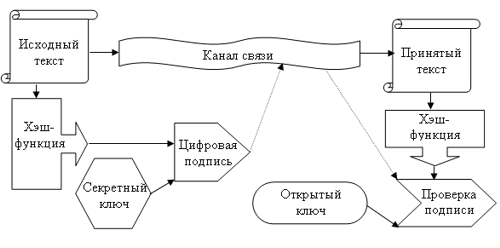
Рис. 3. Алгоритм электронной цифровой подписи

На вход алгоритма поступает файл, необязательно текстовый, основное требование, предъявляемое к входным параметрам ЭЦП, – фиксированная длина, для этого используется хэш-функция.
Теоретически применение различных средств шифрования сулит радужные перспективы всем компаниям, использующим в своей деятельности Интернет, но тут возникает новая проблема – найти компромисс с государством и его законами, данная проблема подробно освещена в [30].
В соответствии с Федеральным законом «Об электронной цифровой подписи» № 1-Ф3 от 10 января 2002 г. электронная цифровая подпись в электронном документе признается равнозначной собственноручной подписи в документе на бумажном носителе. Также обеспечивается правовое регулирование для организации электронного документооборота, распределения открытых и закрытых ключей, построения центров сертификации, определяются ответственности сторон.
Принятие данного закона, хотя в нем есть некоторые неопределенности, позволил регламентировать использование асимметричных средств шифрования, в данном случае ЭЦП, для защиты данных в Интернете.

Литература

1. Shannon C.E. Communication Theory of Secrecy Systems. Bell Systems Technical Journal 28, 1949, p. 656 - 715.
2. Federal Information Processing Standards Publication 46-2. Data Encryption Standard (DES). NIST, US Department of Commerce, Washington D.C, 1993.
3. ГОСТ 28147-89. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования.
4. Bruce Schneier, Applied Cryptography: Protocols, Algorithms and Source Code in C. John Willey & Sons, 1994.
5. Nechvatal James. Public-Key Cryptography. NIST, Gaithersburg, 1990.
6. Weiner M. Efficient DES key search : Technical Report TR-244, School of Computer Science, Carleton University, 1994.
7. Odlyzko A.M. The Future of Integer Factorization. Cryptobytes, RSA Laboratories.- vol. 1, N 2, 1995, p. 5 - 12.
8. Rogaway P. The security of DESX. Cryptobytes, RSA Laboratories, vol. 2, N 2, 1996, p. 8 - 11.
9. Kaliski B., Robshaw M. Multiple encryption: weighing security and perfomance. // Dr. Dobb’s Journal, January 1996, p. 123 - 127.
10. Rivest R.L. The RC5 Encryption Algorithm. Cryptobytes, RSA Laboratories, vol. 1, N 1, 1995, p. 9 - 11.
11. Kaliski B., Yiqun Lisa Yin. On the Security of the RC5 Algorithm. Cryptobytes, RSA Laboratories, vol. 1, N 2, 1995, p. 12.
12. Олейник В. Циклы в алгоритме криптографического преобразования данных ГОСТ 28147-89. http://www.dekart.ru
13. Андрей Винокуров. Алгоритм шифрования ГОСТ 28147-89, его использование и реализация для компьютеров платформы Intel x86.
14. Что такое Blowfish? http://www.halyava.ru/aaalexey/CryptFAQ.html.
15. Linn J. Privacy Enhancement for Internet Electronic Mail: Part I: Message Encryption and Authentication Procedures. RFC 1421, 1993.
16. Евтушенко Владимир. Тройной DES. Новый стандарт? http://www.bgs.ru/russian/security05.html.
17. Что такое ГОСТ28147-89? http://www.halyava.ru/aaalexey/GOST.html.
18. Andrew Jelly. /Криптографический стандарт в новом тысячелетии/, http://www.baltics.ru/~andrew/AES_Crypto.html.
19. Алгоритм шифрования Rijndael. http://www.stophack.ru/spec/rijndael.shtml.

Статья опубликована на сайте: 27.07.2007